MOSFETのイメージ
半導体の話をしていた時に、MOSFETの反転層ができるイメージを図示。
空乏層とか反転層とかイメージしにくいので、身近な例で考えてみた。
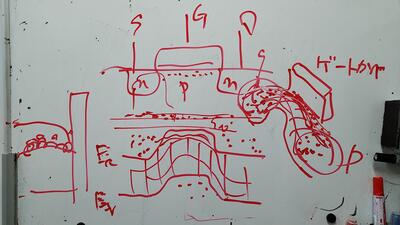
例えて言えば、ブロック塀で支えられて土が詰まれている。ソースとドレイン部分は低く、ゲート部分は高く土が詰まれているところに雨が降ると、ソースドレインの所に水がたまる。ゲートの所は高いのでたまらない。この高さが、伝導体Ecに相当。
そこで地盤沈下かなにか起きてブロック塀が沈下して、塀のきわの土がつられて陥没、ゲート部分が十分ひくくなるとソースドレイン部分にたまった水がそこにも溜まってりだす。
これで表面が反転層になって、電子がたまるイメージ。いま全体的に勾配があると、横に水が流れる。これがVDSの電圧が小さい状態でチャネルに電流が流れるイメージになる。
空乏層とか反転層とかイメージしにくいので、身近な例で考えてみた。
例えて言えば、ブロック塀で支えられて土が詰まれている。ソースとドレイン部分は低く、ゲート部分は高く土が詰まれているところに雨が降ると、ソースドレインの所に水がたまる。ゲートの所は高いのでたまらない。この高さが、伝導体Ecに相当。
そこで地盤沈下かなにか起きてブロック塀が沈下して、塀のきわの土がつられて陥没、ゲート部分が十分ひくくなるとソースドレイン部分にたまった水がそこにも溜まってりだす。
これで表面が反転層になって、電子がたまるイメージ。いま全体的に勾配があると、横に水が流れる。これがVDSの電圧が小さい状態でチャネルに電流が流れるイメージになる。

半導体をちゃんとシミュレーションしようとすると
有償、無償、専用、汎用いろんなツールがありますが、
無料の数値計算ツールでScilabというのがあり、
scilab 半導体 シミュレーション
で検索すると、例えば以下のサイトが見つかりました。
偏微分方程式を解いて半導体中のキャリアの運動を求めているとのことです。
ここでも、物理量の正確さは欠いているいるようですが、私の作ったランダムなツブツブよりも数式的正確さはありそうです。
https://user.numazu-ct.ac.jp/~mochizuki-k/scilab/#j5g
こちらは、真正半導体のフェルミ準位をScilabで解いてます。正確性を求めるとこうなりますね。
http://gomisai.blog75.fc2.com/blog-entry-778.html
ほか、半導体、シミュレーションで画像検索すると、こんな感じの画像を見つけました。
これはもう有償専用パッケージですね。
https://www.msiism.jp/article/semiconductor.html
なんかいろいろできそうな、Nova TCAD の動画解説も貼っておきます。
無料の数値計算ツールでScilabというのがあり、
scilab 半導体 シミュレーション
で検索すると、例えば以下のサイトが見つかりました。
偏微分方程式を解いて半導体中のキャリアの運動を求めているとのことです。
ここでも、物理量の正確さは欠いているいるようですが、私の作ったランダムなツブツブよりも数式的正確さはありそうです。
https://user.numazu-ct.ac.jp/~mochizuki-k/scilab/#j5g
こちらは、真正半導体のフェルミ準位をScilabで解いてます。正確性を求めるとこうなりますね。
http://gomisai.blog75.fc2.com/blog-entry-778.html
ほか、半導体、シミュレーションで画像検索すると、こんな感じの画像を見つけました。
これはもう有償専用パッケージですね。
https://www.msiism.jp/article/semiconductor.html
なんかいろいろできそうな、Nova TCAD の動画解説も貼っておきます。
トランジスタの簡易シミュレーション
20年位前にちぃったpn接合のシミュレーションを元にしてトランジスタの簡易シミュレーションを作りました。
初期値としてベースに順方向、コレクタに逆方向バイアスが適当に入っててスタート。
図のように電子正孔が黒丸、白〇で表示されて動きます。
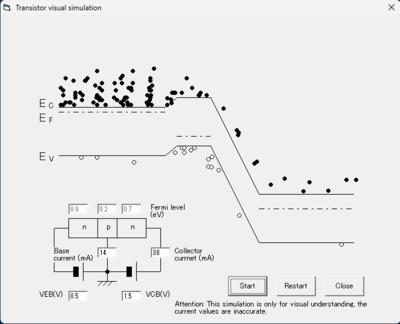
これでわかることは、
1)エミッタ、ベース、コレクタの順に不純物密度が高くなってる。
2)エミッタからベースに電子が流れ込み、ベースからエミッタに正孔が流れ込んでるが、正孔の方が少ない。
3)ベースに流れ込んだ電子は拡散によりコレクタ接合に達すると、電界によりコレクタに吸い出される。
4)エミッタの電子数を一定にしてコレクタに流れていった分をコレクタ電流としてカウントし、ベースの正孔がエミッタに拡散して再結合により消費された分の補充をベース電流としてカウントしている。
5)ベース電流より、コレクタ電流の方が多い。(実際は、けた違いに多いけどこの視覚的なシミュレーションでは数倍程度)
6)コレクタ電圧を大きくしても、右側のエネルギーが低くなるだけで、コレクタ電流の量は原理的にほとんど変化なし。(実際はコレクタ接合の空乏層幅の変化で少し増加)
7)エミッタ電圧を大きくすると、ベースへの流入が増え、それがベースを通り越してコレクタ電流も増える。
電流値は不正確、P,N型領域中の無電界の部分の平衡状態も崩れてしまってます。
簡易的なつくりだけにこのあたりが限界です。これ以上正確性を求めるなら、極端な例外処理をあちこちいれるか、視覚めーじを犠牲にするかですので、ここで改良は終わりにします。
ダウンロードはこちら、transistor.zip
.exeに直リンクを貼ると警告がでるので、zip圧縮しました。警告出ると思いますが一応ウィルスチェックは通したので実行してみてください。
初期値としてベースに順方向、コレクタに逆方向バイアスが適当に入っててスタート。
図のように電子正孔が黒丸、白〇で表示されて動きます。

これでわかることは、
1)エミッタ、ベース、コレクタの順に不純物密度が高くなってる。
2)エミッタからベースに電子が流れ込み、ベースからエミッタに正孔が流れ込んでるが、正孔の方が少ない。
3)ベースに流れ込んだ電子は拡散によりコレクタ接合に達すると、電界によりコレクタに吸い出される。
4)エミッタの電子数を一定にしてコレクタに流れていった分をコレクタ電流としてカウントし、ベースの正孔がエミッタに拡散して再結合により消費された分の補充をベース電流としてカウントしている。
5)ベース電流より、コレクタ電流の方が多い。(実際は、けた違いに多いけどこの視覚的なシミュレーションでは数倍程度)
6)コレクタ電圧を大きくしても、右側のエネルギーが低くなるだけで、コレクタ電流の量は原理的にほとんど変化なし。(実際はコレクタ接合の空乏層幅の変化で少し増加)
7)エミッタ電圧を大きくすると、ベースへの流入が増え、それがベースを通り越してコレクタ電流も増える。
電流値は不正確、P,N型領域中の無電界の部分の平衡状態も崩れてしまってます。
簡易的なつくりだけにこのあたりが限界です。これ以上正確性を求めるなら、極端な例外処理をあちこちいれるか、視覚めーじを犠牲にするかですので、ここで改良は終わりにします。
ダウンロードはこちら、transistor.zip
.exeに直リンクを貼ると警告がでるので、zip圧縮しました。警告出ると思いますが一応ウィルスチェックは通したので実行してみてください。
トランジスタのシミュレーションは途中。
昔のフォルダを調べたら、トランジスタの定性的シミュレーションを作りかけて終わってました。
Visual Basic 6で作ってて、いまはVB6をPCにインストールしてないので続きが作れません。
せっかくなのでトランジスタまではあると良いんですが。
Visual Basic 6で作ってて、いまはVB6をPCにインストールしてないので続きが作れません。
せっかくなのでトランジスタまではあると良いんですが。
pn接合シミュレーション(定性的イメージ)
前の書き込みの続き。
pn接合の定性的なシミュレーションです。これも約20年前に作ったものです。
ゼロバイアスの時が以下の図で、左のn型半導体の部分は電子が多数、右のp型半導体の部分は正孔が多数になってます。この時、例えばn型の電子のエネルギー的に高いところの電子密度がp型の少数キャリアの電子密度と同じくなるようになっています。
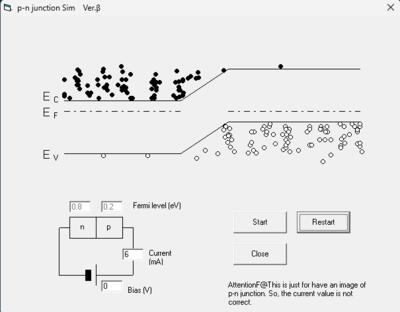
これに順方向バイアス、n型にマイナス、p型にプラスの電圧を加えると図のように、フェルミ順位に差ができてエネルギー障壁(電位障壁)が低くなり、多数キャリアがお互いに逆方向に拡散していき、電子ー正孔の再結合が起こり、順方向電流となります。
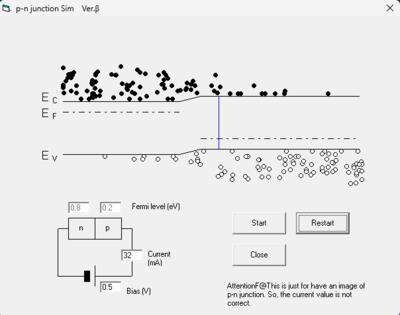
逆方向バイアスの時は、図のようにエネルギー障壁が高くなり、多数キャリアの移動はできなくなります。逆に空乏層近くの少数キャリが逆方向に流れ込んでわずかな逆方向電流となります。
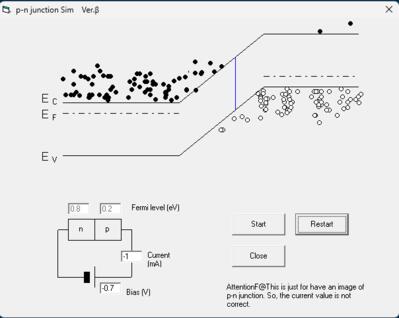
これも、実際の電流スケールはけた違いの現象なので、あくまで定性的、視覚的に示すシミュレーションです。原理的な数式通りにでなく、逆に視覚的に見せるために細工したところが大変だった記憶があります。
ダウンロードはこちら、pn-junctionSim.zip
.exeに直リンクを貼ると警告がでるので、zip圧縮しました。警告出ると思いますが一応ウィルスチェックは通したので実行してみてください。
pn接合の定性的なシミュレーションです。これも約20年前に作ったものです。
ゼロバイアスの時が以下の図で、左のn型半導体の部分は電子が多数、右のp型半導体の部分は正孔が多数になってます。この時、例えばn型の電子のエネルギー的に高いところの電子密度がp型の少数キャリアの電子密度と同じくなるようになっています。

これに順方向バイアス、n型にマイナス、p型にプラスの電圧を加えると図のように、フェルミ順位に差ができてエネルギー障壁(電位障壁)が低くなり、多数キャリアがお互いに逆方向に拡散していき、電子ー正孔の再結合が起こり、順方向電流となります。

逆方向バイアスの時は、図のようにエネルギー障壁が高くなり、多数キャリアの移動はできなくなります。逆に空乏層近くの少数キャリが逆方向に流れ込んでわずかな逆方向電流となります。

これも、実際の電流スケールはけた違いの現象なので、あくまで定性的、視覚的に示すシミュレーションです。原理的な数式通りにでなく、逆に視覚的に見せるために細工したところが大変だった記憶があります。
ダウンロードはこちら、pn-junctionSim.zip
.exeに直リンクを貼ると警告がでるので、zip圧縮しました。警告出ると思いますが一応ウィルスチェックは通したので実行してみてください。




